Rough notes on structured information in CT models
| Created: 07 Jun 2013 | Modified: 23 Jul 2020 | BibTeX Entry | RIS Citation |
The bits of information that go into any real skill, behavior, or complex artifact display many types of semantic relationships. What I’m interested in are classes of relationships among those bits of information, where the classes affect the patterns of spreading, persistence, generative entrenchment, or openness to innovation for the bits of information.
(Aside: I really need a better term for the “bits of information”, because I refuse to call them “memes,” and they’re not really _units_in the observational sense.)
This is just a first set of notes, so I’m not making a claim yet that these are the correct set of minimal classes of relationships. These seem like obvious candidates for exploration, however. Some of these may turn out to have identical distributional consequences, others may differ.
If two semantic relationships have identical distribution consequences, it doesn’t mean that the relationships aren’t an important distinction in cognitive and developmental terms. It simply means that the distinction has equifinalities using distributional measures at population scales.
Classes of Information Relationships
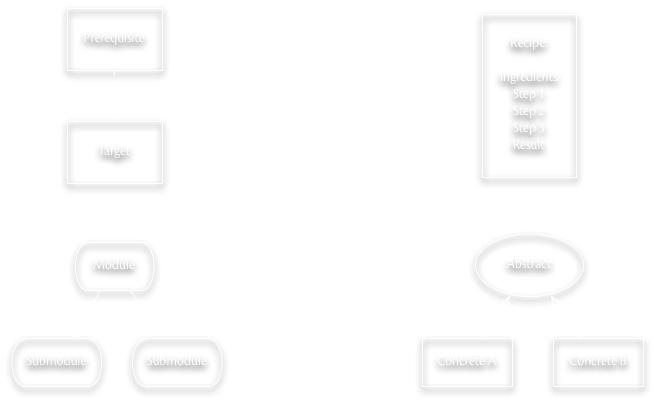
Our knowledge (about skills and artifacts) is clearly modular in many respects, although it often doesn’t start out that way. Prototypes are often simply the result of some trial and error and directed learning, and we “modularize” the results when we’re trying to package it up to “assembly line” it or teach it. But by the time a skill or artifact is widespread within a population, you can bet that its components are at least weakly modularized, especially if there are specializations involved in production or construction.
Recipes are often composed of modules, but the recipe itself is algorithmic in a way that modules themselves need not be. Many artifact production processes are actually combinations of recipes that specify steps which are modular and possibly involve sub-steps and sub-modules, for example.
Prerequisite information and widely used modules are key examples of generative entrenchment in cultural information. Such information has deep persistence and often resistance to alteration (although we often repackage it in synonymous or equivalent ways to enhance its learnability or reduce the skill level required to employ it). I would expect that prerequisites are essentially “pleiotropic” with the target knowledge it enables, but given that a prereq can support multiple pieces of knowledge, we’ll see prereqs regularly outliving many of the targets they support.
Abstraction is another important way in which we increase the scope of learning – instead of teaching redundant information for every concrete case, we often abstract out the common elements and learn them separately. This may be a very late element in cultural learning, but I need to think more about that. Think about learning electrical engineering – we teach principles of circuit design and electronics, which students can then apply to constructing a radio or other device.
Abstractions are then ripe for being turned into prerequisites, of course…
Model Notes
Mesoudi and O’Brien (2008) addressed hierarchical knowledge, and its relative performance with respect to non-hierarchical knowledge, in a social learning process. That investigation showed that hierarchical (i.e., modular, tree-like) structures outperformed “all at once” or piecemeal knowledge learning particularly when there were a limited number of learning trials within which to achieve competency.
If we assume a pool of cultural information which are related in modular ways, with varying depth and size, and if artifacts are constructed using pieces of varying size, what is the distribution of lifetimes for the combinations of modules? In order to make this meaningful, we have to construct a rule for mutation that determines the level(s) at which random changes can occur. For example, a mutation at level N might have to replace N and its submodules? But a mutation at N in a submodule would not replace supermodule at N-1, and thus sibling module trees. This seems like a good simple experiment to run, in comparison to WFIA, which would seem to be a good neutral model of nonhierarchical, diffusionist (in the M&O 2008 sense) transmission. Taking actual performance out of the mix, if we have modular mutation and copying, how does this change the basic statistics of trait persistence and frequency distribution?
Recipes should create correlations between items, so the hard bit is determining if there’s any way to differentiate recipes from modules just with frequency/timing data. Or are recipes and modular information really just the same thing, with different packaging? In capturing the dynamics of modular information in an abstract way, does it capture all structured relationships, from the perspective of frequency patterns?
